随机变量及其分布
随机变量及其分布
分布函数: def:F(x)=P(X≤x)
离散分布
- 二项分布: X∼B(n,p)
- P(X=k)=Cnkpk(1−p)n−k(k=0,1,…,n)
- EX=np, VarX=np(1−p)
- 几何分布: X∼Ge(p)
- P(X=k)=(1−p)k−1p(k=1,2,…)
- EX=p1, VarX=p21−p
- 泊松分布: X∼P(λ)
- P(X=k)=k!λke−λ(k=0,1,2,…)
- EX=λ, VarX=λ
- 泊松定理: X∼B(n,p)np→λ,n很大近似X∼P(np)
连续分布
均匀分布: X∼U(a,b)
- f(x)={b−a10a<x<b余
- EX=2a+b
- VarX=12(b−a)2
- F(x)=⎩⎨⎧0b−ax−a1x<aa≤x<bx≥b
指数分布: X∼E(λ)
- f(x)={λe−λx0x>0余
- EX=λ1
- VarX=λ21
- F(x)={1−e−λx0x>0x≤0
- tips:指数分布具有无记忆性,即 P(X>s+t∣X>s)=P(X>t)
① 问“小于” (X≤x):即“在 x 时间前坏掉/发生”的概率:
F(x)=P(X≤x)=1−e−λx
② 问“大于” (X>x):即“活过 x 时间 / 至少能用 x 小时”的概率(这叫生存函数):
P(X>x)=e−λx
正态分布: X∼N(μ,σ2)
- f(x)=2πσ1e−2σ2(x−μ)2−∞<x<+∞
- EX=μ, VarX=σ2
- 标准正态分布: X∼N(0,1), φ(x)=2π1e−2x2
- F(x)=P(X≤x)=P(σX−μ≤σx−μ)=Φ(σx−μ)
- 性质: Φ(−a)=1−Φ(a), Φ(0)=21, P(∣X∣≤a)=2Φ(a)−1
if f(x)=Aeax+bx+c (x∈(a,b)(or)x∈(−∞,+∞)) 则为正态
随机变量函数的分布
- 命题: FY(y)=P(Y≤y)=P(g(X)≤y)=∫g(x)≤yfX(x)dx
- 定理: X 的密度函数 fX(x) 在 (a,b) 之间严格单调,则 Y=f(X) 服从 (a,b) 上的分布:
- 0≤y≤1: fY(y)=P(∣y∣)=P(F−1(y))∣(F−1)′(y)∣
- =P∣X≤F−1(y)∣=F(F−1(y))=y (均匀分布)
- 一般地:fY(y)=fX[h(y)]⋅∣h′(y)∣ (其中 x=h(y) 是反函数)
多维随机变量及分布
F(x,y)=P(X≤x,Y≤y)
- 性质:
- F(+∞,+∞)=1, F(−∞,+∞)=0, F(+∞,−∞)=0
- 非负性、规范性、单调不减性、右连续性
- P(x1<X≤x2,y1<Y≤y2)=F(x2,y2)−F(x1,y2)−F(x2,y1)+F(x1,y1)
二维连续
- F(x,y)=∫−∞x∫−∞yf(u,v)dudv
- P((X,Y)∈G)=∬Gf(x,y)dxdy
边缘概率密度
- fX(x)=∫−∞+∞f(x,y)dy
- fY(y)=∫−∞+∞f(x,y)dx
条件概率密度
- fX∣Y(x∣y)=fY(y)f(x,y) 为在 Y=y 条件下 X 的概率密度(要写出来)
独立性
f(x,y)=fX(x)⋅fY(y)
二维均匀分布
A=SD, f(x,y)={SD10(x,y)∈D余
性质:
- (X,Y) 在 D={(x,y)∣a≤x≤b,c≤y≤d} 上服从二维均匀分布 ⟺X∼U(a,b),Y∼U(c,d)
- (X,Y)∈G,P((X,Y)∈G)=SDSG
- But!!! (X,Y) 服从二维均匀分布 ⇏X,Y 服从一维均匀分布 (反之亦然)
二维正态、极值、可加性与数字特征
二维正态分布: (X,Y)∼N(μ1,μ2;σ12,σ22;ρ)性质:
- 边缘分布是正态分布 X∼N(μ1,σ12), Y∼N(μ2,σ22)
- X 与 Y 相互独立之充要条件 ρ=0
- aX+bY∼N(aμ1+bμ2,a2σ12+b2σ22+2abρσ1σ2)
- 条件分布正态分布
- (aX+b,cY+d) 也服从二维正态。∣acbd∣=0
计算: X1∼N(μ1,σ12) 且相互独立 ∑aiXi∼N(∑aiμi,∑ai2σi2)
二维随机变量函数分布
FZ(z)=P(Z≤z)=P(X+Y≤z)=∬x+y≤zf(x,y)dxdy
两种方法,一种分布函数法,普遍适用,如果相互独立,可以卷积
如果 X 和 Y 独立,我们可以跳过二重积分,直接套单重积分公式。
卷积公式:
fZ(z)=∫−∞+∞fX(x)⋅fY(z−x)dx
两个坑
- fY(z−x) 是啥? 就是把 fY(y) 里的 y 替换成 z−x。
- 积分限怎么定?
- 公式写的是 −∞ 到 +∞,但实际上要看 fX(x) 和 fY(z−x) 哪里不为 0
- 我们要找这两个函数“非零区域”的交集
最大值最小值分布
X1…Xn 相互独立
- U=max{X1…Xn}
- Fmax(z)=FX1(z)FX2(z)…FXn(z)
- if iid Fmax(z)=[F(z)]n
- V=min{X1…Xn}
- Fmin(z)=1−[1−FX1(z)][1−FX2(z)]…[1−FXn(z)]
- if iid Fmin(z)=1−[1−F(z)]n
具有可加性的分布
- Xi∼B(ni,p)⇒X1+X2+⋯+Xn∼B(n1+⋯+nk,p)
- (独立同分布)
- Xi∼P(λi)⇒X1+X2+⋯+Xk∼P(λ1+⋯+λk)
- Xi∼N(μi,σi2)⇒a1X1+a2X2+⋯+akXk∼N(∑aiμi,∑ai2σi2)
- Xi∼χ2(ni)⇒X1+X2+⋯+Xk∼χ2(n1+n2+⋯+nk)
- Xi∼E(λ)⇒min(X1,X2…Xk)∼E(λ1+λ2+⋯+λk)
数字特征
- 期望:性质:E(c)=c, E(cX)=cE(X), E(X+c)=E(X)+c, X,Y 相互独立 E(XY)=E(X)E(Y)
- 方差:性质:Var(c)=0, Var(cX)=c2VarX, if X,Y 相互独立 Var(X±Y)=VarX+VarY
- 切比雪夫不等式: def:P(∣X−EX∣≥ε)≤ε2VarX
协方差、相关系数、大数定律
协方差
def:Cov(XY)=E(XY)−EX⋅EY
性质:
- Cov(X,X)=Cov(Y,Y)
- Cov(X,c)=0
- Cov(aX,bY)=abCov(X,Y)
- Cov(X±Y,Z)=Cov(X,Z)+Cov(Y,Z)
- if X,Y 独立 Cov(X,Y)=0
- Var(X±Y)=VarX+VarY±2Cov(X,Y)
- Cov(X,X)=VarX
相关系数
def:ρXY=Corr(X,Y)=VarXVarYCov(X,Y)
- if Corr(X,Y)=0 则 X,Y 不相关
性质:
- ∣ρXY∣≤1, ρXX=ρYX, ρXX=1
- ∣ρXY∣=1⟺P(Y=aX+b)=1
- ∣ρXY∣ 越接近1,表明 X,Y 的线性相关程度越大
- 只有当 (X,Y)∼N,独立 ⟺ 不相关
大数定律和中心极限定理
大数定律
def:limn→∞P(∣Xn−a∣≥ε)=0⇒XnPa (依概率收敛)
性质: XnPa, 则 g(Xn)Pg(a) (g(x) 在 a 处连续)
切比雪夫大数定律: X1…Xn 两两不相关,且 VarXn 一致有界。 XˉPEXˉ
- limn→∞P(∣n1∑Xi−n1∑EXi∣<ε)=1.
(常用) 辛钦大数定律: 1∘X1…Xn iid 2∘EXi=μ 存在。
- XˉPμ, limn→∞P(∣n1∑Xi−μ∣<ε)=1
列维-林德伯格定理: X1…Xn iid, EXk=μ,VarXk=σ2>0
- 即:∑Xi近似N(nμ,nσ2)
- nσ∑Xi−nμ=σ/nXˉ−μ近似(0,1).
- 棣莫弗-拉普拉斯定理: Xn∼B(n,p), Xnn→∞N(np,np(1−p))
抽样分布、Fisher定理
常用统计量的数字特征
1. 样本均值
X=n1i=1∑nXi;
2. 样本方差
S2=n−11i=1∑n(Xi−X)2;
- 样本标准差
S=n−11i=1∑n(Xi−X)2;
5个常用结论
X1,X2,⋯,Xn 为来自总体 X 的样本,EX=μ,VarX=σ2
EXi=μ,VarXi=σ2;
EX=μ,VarX=nσ2;
ES2=σ2 ,VarS2=n−12σ4
三大抽样分布
- χ2 分布: def: X1…Xn 相互独立 N(0,1),相互独立。则 χ2=X12+⋯+Xn2
- χ2∼χ2(n)
- Eχ2=n, Varχ2=2n
- 性质:可加性: χ12∼χ2(n1),χ22∼χ2(n2) 且独立,则 χ12+χ22∼χ2(n1+n2)
- t 分布: def:X∼N(0,1),Y∼χ2(n), X,Y 独立。
- t=Y/nX∼t(n) (自由度为 n 的 t 分布)
- 性质: t 分布的概率密度是偶函数
- F 分布: def:X∼χ2(n1),Y∼χ2(n2), X,Y 独立
- F=Y/n2X/n1∼F(n1,n2)
- 性质: 1)F∼F(n1,n2)⇒F1∼F(n2,n1), 2)X∼t(n)⇒X2∼F(1,n).
正态总体抽样分布
def:X1…Xn 来自 N(μ,σ2),xˉ=n1∑Xi,S2=n−11∑(Xi−xˉ)2
- 1):xˉ∼N(μ,nσ2), (xˉ−μ)n/σ∼N(0,1)
- 2):xˉ 与 S2 相互独立
- 3):σ2(n−1)S2=σ2∑(Xi−xˉ)2∼χ2(n−1); σ2∑(Xi−μ)2∼χ2(n).
- 4):T=S/nxˉ−μ∼t(n−1)
参数估计
点估计
- 矩估计法:n1∑XikPEXk, n1∑(Xi−xˉ)kPE(X−EX)k
最大似然估计:
离散型总体 若总体 X 的分布律为 P(X=x)=p(x;θ),则似然函数为:
L(θ)=i=1∏np(xi;θ)
连续型总体 若总体 X 的概率密度函数为 f(x;θ),则似然函数为:
L(θ)=i=1∏nf(xi;θ)
第一步:构造似然函数 写出样本的联合概率分布(或联合密度函数):
L(θ)=i=1∏np(xi;θ)或i=1∏nf(xi;θ)
第二步:取对数 为了简化计算(将连乘 ∏ 转化为求和 ∑,方便求导),对 L(θ) 取自然对数:
lnL(θ)=i=1∑nlnp(xi;θ)或i=1∑nlnf(xi;θ)
第三步:建立似然方程并求解 对 θ 求导,并令导数为 0(寻找驻点):
dθd[lnL(θ)]=0
解出的 θ^ 即为最大似然估计值。
似然函数单调的用次序统计量
估计量的评价标准 区间估计
估计量的评价标准:
- 无偏性: E(θ^)=θ⇒ 无偏估计
- 有效性: Varθ^1<Varθ^2,则 θ^1 更有效。
- 相合性: θ^Pθ
区间估计:枢轴量
| 待估参数 | 已知条件 | 枢轴量 & 分布 | 置信区间 (1−α) |
|---|
| μ | σ2 已知 | σ/nXˉ−μ∼N(0,1) | (xˉ−u2αnσ,xˉ+u2αnσ) |
| μ | σ2 未知 | S/nXˉ−μ∼t(n−1) | (xˉ−t1−2α(n−1)nS,xˉ+t1−2α(n−1)nS) |
| σ2 | μ 已知 | σ2∑i=1n(Xi−μ)2∼χ2(n) | (χ1−2α2(n)∑i=1n(Xi−μ)2,χ2α2(n)∑i=1n(Xi−μ)2) |
| σ2 | μ 未知 | σ2(n−1)S2∼χ2(n−1) | (χ1−2α2(n−1)(n−1)S2,χ2α2(n−1)(n−1)S2) |
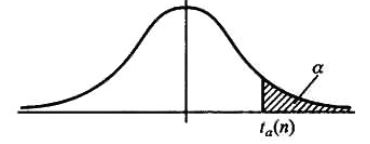
算单侧的把2α换成α
次序统计量:
最小值分布 (记为 X(1) 或 min):
FX(1)(x)=1−{1−F(x)}n
最大值分布 (记为 X(n) 或 max):
FX(n)(x)=[F(x)]n